In this post we’ll play with GHC’s new LLVM code generator backend, and see how much faster some Haskell programs are when compiled with LLVM instead of GCC.
For the kind of loops we get from stream fusion, the -fllvm backend produced a lot better code, up to 3x faster in some cases. There are pretty graphs, and some smoking hot new technology.
Overview
This week David Terei announced that his work on an LLVM code generator backend for the Glasgow Haskell Compiler was ready to try out. Initial reports from his undergraduate thesis held that the LLVM code generator was competitive with the current GHC native code generator, a bit slower than the C backend in general (which uses GCC for code generation), but, tantalisingly, should produce big speedups for particular Haskell programs. In particular, tight loops of the kind generated by the bytestring, vector, data parallel arrays or text libraries. David reported speedups of 25% over the previous best performance we’d got from GHC for data parallel code.
I was very keen to try it out on the vector library — a fast, fusible numerical arrays package (similar to NumPy), which generates some very tight loops. Under the C backend, GCC has been failing to spot that the code GHC generates were actually loops, and this lead to GCC optimizing the generated code pretty badly. The native code generator does ok, but doesn’t have a lot of the clever low-level optimizations we need for really good bare metal performance.
So how would the new LLVM backend do?
Setting up
To try out the LLVM backend I followed the instructions on the wiki.
- Check out GHC HEAD from darcs.
- Apply the LLVM patch.
- Check out LLVM from svn
- Apply the GHC patch
- Build your GHC.
This worked out of the box, and I now have a GHC 6.13 with the -fllvm flag.
$ ghc --info
[("Project name","The Glorious Glasgow Haskell Compilation System")
,("Project version","6.13.20100221")
,("Booter version","6.12.1")
,("Stage","2")
,("Have interpreter","YES")
,("Object splitting","YES")
,("Have native code generator","YES")
,("Have llvm code generator","YES")
,("Support SMP","YES")
,("Unregisterised","NO")
,("Tables next to code","NO")
,("Win32 DLLs","")
,("RTS ways","l debug thr thr_debug thr_l ")
,("Leading underscore","NO")
,("Debug on","False")
,("LibDir","/home/dons/lib/ghc-6.13.20100221")
]
Running on a dual core Core 2 laptop:
$ uname -msr Linux 2.6.32-ARCH x86_64
You can then install packages as normal, via cabal, and add the -fllvm flag to see GHC build things via the new backend:
$ cabal install primitive --ghc-options=-fllvm
The packages I’m interested in are:
- The darcs version of the vector package.
And some helper code in:
I also modifed the ghc-core tool to support showing the LLVM generated assembly.
Warm up lap
Let’s check the backend is working (remember to add the -fllvm flag):
$ ghc -O2 --make A.hs -fllvm -fforce-recomp [1 of 1] Compiling Main ( A.hs, A.o ) Linking A ... $ time ./A "hey" ./A 0.00s user 0.00s system 61% cpu 0.005 total
Good! The LLVM backend is generating working code for x86_64/Linux. Now, something more ambitious … a program from the shootout.
A shootout program
So let’s find some code that’s already been optimized. I’l compile the pidgits shootout benchmarks (where Haskell’s already the fastest entry).
First, with the native code gen:
$ ghc -O2 -fasm A.hs –make -fforce-recomp
$ time ./A 10000 > /dev/null
./A 10000 > /dev/null 3.19s user 0.03s system 91% cpu 3.509 total
With the old GCC backend:
$ ghc -O2 -fvia-C -optc-O3 A.hs –make -fforce-recomp
$ time ./A 10000 > /dev/null
./A 10000 > /dev/null 2.89s user 0.03s system 97% cpu 2.988 total
And with the -fllvm backend:
$ ghc -O2 -fllvm A.hs –make -fforce-recomp
$ time ./A 10000 > /dev/null
./A 10000 > /dev/null 2.86s user 0.02s system 98% cpu 2.936 total
Woo. It runs, and we get a speedup! Now for some serious business.
The Vector Package
Vector is a Haskell library for working with arrays. It provides several array types (boxed, unboxed, C), with a rich interface similar to the lists library, and some functions reminiscent of Data Parallel Haskell. There’s a tutorial on how to use it.
The interface is built entirely around stream fusion combinators — a general form of classic loop fusion made possible by purity. When you do multiple passes over the data (e.g. sum/map/fold/filter/…) the compiler will common up the loops, and discard intermediate arrays, making the code potentially very fast.
The loops that are generated tend to be very register heavy, do no heap allocation, and benefit from clever imperative loop optimizations. Unfortunately, the GCC backend to GHC doesn’t spot that these are actually loops, so doesn’t get to fire many optimizations.
The promise of the LLVM backend is that it will recognize the loops GHC generates from fused code. Let’s see how it performs.
To benchmark these programs, I’ll use the criterion and progression benchmarking libraries. (I had to build the darcs version of gtk2hs, and compiler data accessor-template with the -ftemplate_2_4 flag)
Simple loops
To start off, let’s generate 1 billion ints, sum them, print the result. That should tell us if our loops are efficient:
import qualified Data.Vector as U main = print . U.sum $ U.enumFromTo 1 (1000000000 :: Int)
There are two loops in this program. enumFromTo and sum.
The core
GHC compiles these two loops into a single loop, when compiled with -O2 or -Odph:
loop :: Int# -> Int# -> Int#
loop x y =
case <=# y 1000000000 of
False -> x
True -> loop (x +# y) (y +# 1)
This is perfect. We write “sum (enumFromTo 1 n)” and we get a non-allocating loop.
The native backend
GHC 6.13 with the native code generator generates the following assembly for the inner loop:
Main_mainzuzdszdwfoldlMzqzuloop_entry: .Lc21u: cmpq $1000000000,%rsi jle .Lc21x movq %r14,%rbx movq (%rbp),%rax jmp *(%rax) .Lc21x: addq %rsi,%r14 incq %rsi jmp Main_mainzuzdszdwfoldlMzqzuloop_entry
which runs in:
$ time ./enum 500000000500000000 ./enum 1.00s user 0.00s system 99% cpu 1.008 total
The C backend
GHC 6.12.1 with the C backend, (-fvia-C -optc-O3) (I’m having trouble linking programs with the C backend and GHC 6.13), yields a pretty small loop:
Main_mainzuzdszdwfoldlMzqzuloop_info: cmpq $1000000000, %r14 movq %r14, %rax jle .L2 movq %rsi, %rbx jmp *(%rbp) .L2: leaq 1(%r14), %r14 addq %rax, %rsi jmp Main_mainzuzdszdwfoldlMzqzuloop_info
Which runs slower than the native code generator:
$ time ./enum 500000000500000000 ./enum 1.09s user 0.00s system 99% cpu 1.100 total
The LLVM backend
With -O2 -fllvm we get very different code, and it is a bit harder to work out what is going on. LLVM transforms the code far more aggressively.
.LBB1_2: leaq 1(%rsi), %rax addq %rsi, %r14 cmpq $1000000001, %rax jge .LBB1_5 # loop exit addq $2, %rsi addq %rax, %r14 .LBB1_1: # %tailrecurse cmpq $1000000001, %rsi jl .LBB1_2
And the proof is in the pudding:
$ time ./enum 500000000500000000 ./enum 0.48s user 0.01s system 99% cpu 0.488 total
This is the fastest Haskell we’ve ever generated for this little benchmark (at least without manual loop unrolling)!
The LLVM backend more than halved the running time for this simple loop. But remember: general benchmarks aren’t seeing these kind of speedups — LLVM is really excelling itself at the tight numeric code.
Here’s the data presented in a slightly different form, with criterion and progression. The numbers are slightly different, since we won’t inline the length of the vector argument, and we’re wrapping the code in benchmarking wrappers. I wasn’t able to get -fvia-C programs to link under the HEAD, so we’ll exclude those from graphs, but report them in text form.
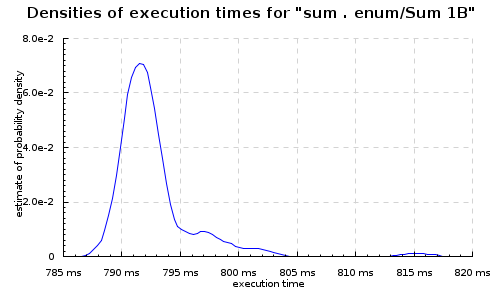
With the -fasm backend:
With the LLVM backend:
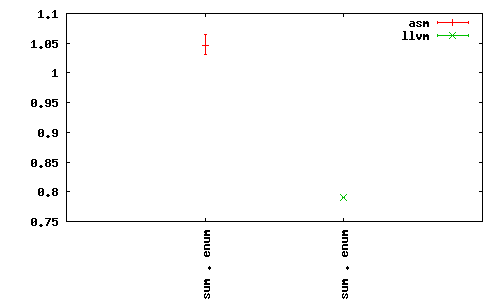
Or side-by-side with the progression package:
The -fasm backend under the progression tool ran around ~1s for each billion ints, while -fllvm was around 0.8s. Note that we get slightly different timings with the loops under each benchmarking tool, due to how the benchmark program and wrapper are optimized.
Zips
Zips are another good candidate, since they turn into nested loops. So, e.g.
import qualified Data.Vector as U
import Data.Bits
main = print . U.sum . U.map (`shiftL` 1) $ U.zipWith (*)
(U.enumFromTo 1 (100000000 :: Int))
(U.replicate (100000000 :: Int) 42)
Which fuses to this set of loops:
loop :: Int# -> Int# -> Int# -> Int#
loop =
\ (sc_s29b :: Int#)
(sc1_s29c :: Int#)
(sc2_s29d :: Int#) ->
case <=# sc1_s29c 100000000 of _ { False -> sc_s29b;
True ->
case <=# sc2_s29d 0 of _ { False ->
loop
(+#
sc_s29b (uncheckedIShiftL# (*# sc1_s29c 42) 1))
(+# sc1_s29c 1)
(-# sc2_s29d 1);
True -> sc_s29b
}
}
Which, again, is perfect Core. All those functions combined into a single non-allocating loop.
-fasm:
Main_mainzuzdszdwfoldlMzqzuloop_entry:
.Lc2aC:
cmpq $100000000,%rsi
jle .Lc2aE
movq %r14,%rbx
movq (%rbp),%rax
jmp *(%rax)
.Lc2aE:
testq %rdi,%rdi
jle .Lc2aH
movq %rsi,%rax
imulq $42,%rax
shlq $1,%rax
addq %rax,%r14
incq %rsi
decq %rdi
jmp Main_mainzuzdszdwfoldlMzqzuloop_entry
.Lc2aH:
movq %r14,%rbx
movq (%rbp),%rax
jmp *(%rax)
Which is reasonable:
$ time ./zipwith
420000004200000000
./zipwith 0.24s user 0.00s system 99% cpu 0.246 total
With the -fvia-C -optc-O3 backend, just the inner loop, since that’s easy to read:
Main_mainzuzdszdwfoldlMzqzuloop_info:
cmpq $100000000, %rsi
jg .L6
.L2:
testq %r14, %r14
jle .L6
leaq (%rsi,%rsi,4), %rcx
leaq -1(%r14), %r14
leaq (%rsi,%rcx,4), %rcx
leaq 1(%rsi), %rsi
leaq (%rdi,%rcx,4), %rdi
jmp Main_mainzuzdszdwfoldlMzqzuloop_info
Which runs in about the same time as the -fasm backend:
$ time ./zipwith 420000004200000000 ./zipwith 0.25s user 0.00s system 99% cpu 0.251 total
With -fllvm the code is wildly different, and I find it pretty hard to reconstruct what transformatoins LLVM has done.
Main_mainzuzdszdwfoldlMzqzuloop_entry:
# BB#0: # %c2cf
subq $8, %rsp
imulq $84, %rsi, %rax
jmp .LBB1_1
.LBB1_3: # %n2cN
# in Loop: Header=BB1_1 Depth=1
incq %rsi
decq %rdi
addq %rax, %r14
addq $84, %rax
.LBB1_1: # %tailrecurse
# =>This Inner Loop Header: Depth=1
cmpq $100000001, %rsi # imm = 0x5F5E101
jge .LBB1_4
# in Loop: Header=BB1_1 Depth=1
testq %rdi, %rdi
jg .LBB1_3
.LBB1_4: # %n2ck
movq (%rbp), %rax
movq %r14, %rbx
movq (%rax), %r11
addq $8, %rsp
jmpq *%r11 # TAILCALL
The “inner loop” is interesting. Nothing like what -fasm or -fvia-C generate. And it’s way faster:
$ time ./zipwith
420000004200000000
./zipwith 0.15s user 0.00s system 99% cpu 0.154 total
So yeah, 40% faster!
Criterion
Here, under criterion (same code, but different values of n), With the -fasm backend, mean execution time 186ms:
With the -fllvm backend, 135 ms (27% improvement):
zipwith3
Heavily nested zips are probably the best cases for LLVM, and we see the -fllvm backend do some pretty wild stuff with this:
import qualified Data.Vector.Unboxed as U import Data.Bits main = print . U.sum $ U.zipWith3 (\x y z -> x * y * z) (U.enumFromTo 1 (100000000 :: Int)) (U.enumFromTo 2 (100000001 :: Int)) (U.enumFromTo 7 (100000008 :: Int))
Which fuses to:
main_$s$wfoldlM'_loop [Occ=LoopBreaker]
:: Int# -> Int# -> Int# -> Int# -> Int#
main_$s$wfoldlM'_loop =
\ (sc_s2jh :: Int#)
(sc1_s2ji :: Int#)
(sc2_s2jj :: Int#)
(sc3_s2jk :: Int#) ->
case sc_s2jh;
True ->
case sc_s2jh;
True ->
case sc_s2jh;
True ->
main_$s$wfoldlM'_loop
(+#
sc_s2jh (*# (*# sc1_s2ji sc2_s2jj) sc3_s2jk))
(+# sc1_s2ji 1)
(+# sc2_s2jj 1)
(+# sc3_s2jk 1)
}
}
}
Great core. With the -fasm backend:
Main_mainzuzdszdwfoldlMzqzuloop_entry:
.Lc2lq:
cmpq $100000000,%rsi
jle .Lc2ls
movq %r14,%rbx
movq (%rbp),%rax
jmp *(%rax)
.Lc2ls:
cmpq $100000001,%rdi
jle .Lc2lu
movq %r14,%rbx
movq (%rbp),%rax
jmp *(%rax)
.Lc2lu:
cmpq $100000008,%r8
jle .Lc2lx
movq %r14,%rbx
movq (%rbp),%rax
jmp *(%rax)
.Lc2lx:
movq %rdi,%rax
imulq %r8,%rax
movq %rsi,%rcx
imulq %rax,%rcx
addq %rcx,%r14
incq %rsi
incq %rdi
incq %r8
jmp Main_mainzuzdszdwfoldlMzqzuloop_entry
Straight forward, and running it:
$ time ./zipwith3 3541230156834269568 ./zipwith3 0.47s user 0.01s system 98% cpu 0.484 total
With -fvia-C -optc-O3:
Main_mainzuzdszdwfoldlMzqzuloop_info:
.text
.p2align 4,,15
.text
.align 8
.type Main_mainzuzdszdwfoldlMzqzuloop_info, @function
# 38 "/tmp/ghc10013_0/ghc10013_0.hc" 1
# 0 "" 2
cmpq $100000000, %rdi
jg .L9
.L4:
cmpq $100000001, %rsi
jg .L9
.L5:
cmpq $100000008, %r14
.p2align 4,,5
jg .L9
.L7:
movq %rsi, %r10
leaq 1(%rsi), %rsi
imulq %rdi, %r10
leaq 1(%rdi), %rdi
imulq %r14, %r10
leaq 1(%r14), %r14
leaq (%r10,%r8), %r8
jmp Main_mainzuzdszdwfoldlMzqzuloop_info
And we get a faster result:
$ time ./zipwith3 3541230156834269568 ./zipwith3 0.34s user 0.00s system 99% cpu 0.344 total
-fllvm, looks like some heavy loop unrolling:
Main_mainzuzdszdwfoldlMzqzuloop_entry: # @Main_mainzuzdszdwfoldlMzqzuloop_entry
# BB#0: # %c2oz
subq $56, %rsp
cmpq $100000002, %rdi # imm = 0x5F5E102
movl $100000002, %eax # imm = 0x5F5E102
movq $-2, %rdx
movq %r9, 40(%rsp) # 8-byte Spill
movq %r15, 48(%rsp) # 8-byte Spill
movq $-3, %r9
movq %r12, 32(%rsp) # 8-byte Spill
movq %r8, %rbx
movq %r13, 24(%rsp) # 8-byte Spill
movq %r14, 16(%rsp) # 8-byte Spill
leaq 1(%rdi), %r13
cmovgq %rdi, %rax
negq %rax
leaq -1(%rdi,%rax), %rcx
cmpq $100000009, %r8 # imm = 0x5F5E109
movl $100000009, %eax # imm = 0x5F5E109
cmovgq %r8, %rax
negq %rax
leaq -1(%r8,%rax), %rax
cmpq %rcx, %rax
cmovaq %rax, %rcx
cmpq $100000001, %rsi # imm = 0x5F5E101
movl $100000001, %eax # imm = 0x5F5E101
cmovgq %rsi, %rax
negq %rax
leaq -1(%rsi,%rax), %rax
cmpq %rax, %rcx
cmovbeq %rax, %rcx
imulq %rdi, %rbx
imulq %rsi, %r13
movq %rcx, %r10
subq %rcx, %rdx
subq %rcx, %r9
imulq %rsi, %rbx
addq %rdi, %r13
notq %r10
movq %r10, %rax
imulq %r10, %rbx
mulq %rdx
addq 16(%rsp), %rbx # 8-byte Folded Reload
movq %rax, %r11
movq %rdx, %r15
movq %r15, %r12
movq %r11, %rax
andq $1, %r15
imulq %r9, %r12
mulq %r9
shldq $63, %r11, %r15
leaq (%r8,%rdi), %r9
addq %rdx, %r12
movq $-4, %rdx
addq %rsi, %r9
subq %rcx, %rdx
movq %r12, %r14
andq $1, %r12
leaq 6(%r9,%r9), %r10
movabsq $6148914691236517205, %r9 # imm = 0x5555555555555555
movq %rdx, 8(%rsp) # 8-byte Spill
imulq %rdx, %r14
leaq 1(%rdi,%rsi), %rdx
shldq $63, %rax, %r12
imulq %r8, %rdx
imulq %r12, %r10
leaq 1(%rdx,%r13), %rdx
imulq %r10, %r9
imulq %r15, %rdx
addq %rdx, %rbx
mulq 8(%rsp) # 8-byte Folded Reload
subq %r9, %rbx
movq %r8, %r9
decq %r8
subq %rcx, %r9
addq %rdx, %r14
movq %rdi, %rdx
decq %r9
shldq $62, %rax, %r14
movq %rsi, %rax
subq %rcx, %rdx
andq $-2, %r14
subq %rcx, %rax
decq %rdx
addq %rbx, %r14
decq %rax
.align 16
.LBB2_1: # %tailrecurse
# =>This Inner Loop Header: Depth=1
cmpq $100000001, %rsi # imm = 0x5F5E101
jge .LBB2_4
# BB#2: # %c2oD
# in Loop: Header=BB2_1 Depth=1
cmpq $100000002, %rdi # imm = 0x5F5E102
jge .LBB2_4
# BB#3: # %c2p5
# in Loop: Header=BB2_1 Depth=1
incq %rsi
incq %rdi
incq %r8
cmpq $100000009, %r8 # imm = 0x5F5E109
jl .LBB2_1
.LBB2_4: # %n2oE
movq (%rbp), %rcx
movq %r9, %r8
movq 24(%rsp), %r13 # 8-byte Reload
movq 32(%rsp), %r12 # 8-byte Reload
movq %r14, %rbx
movq %rax, %rsi
movq %rdx, %rdi
movq 40(%rsp), %r9 # 8-byte Reload
movq 48(%rsp), %r15 # 8-byte Reload
movq (%rcx), %r11
addq $56, %rsp
jmpq *%r11 # TAILCALL
And blows them all out of the water! 3x faster than -fasm! Twice as fast as -fvia-C -optc-O3.
$ time ./zipwith3 3541230156834269568 ./zipwith3 0.16s user 0.00s system 99% cpu 0.158 total
From the Statistics package
The statistics package has some more “realistic” microbenchmarks. Let’s look at those. First, computing the mean of a large array of doubles (here all set to ‘pi’).
main = print (mean (V.replicate 1000000000 (pi :: Double)))
With the -fasm backend:
Main_mainzuzdszdwfoldlMzuloop_entry:
.Lc2b2:
testq %rsi,%rsi
jle .Lc2b5
cvtsi2sdq %r14,%xmm0
movsd .Ln2b8(%rip),%xmm7
subsd %xmm5,%xmm7
divsd %xmm0,%xmm7
addsd %xmm7,%xmm5
incq %r14
decq %rsi
jmp Main_mainzuzdszdwfoldlMzuloop_entry
Simple, easy.
$ time ./mean 3.141592653589793 ./mean 5.58s user 0.01s system 99% cpu 5.599 total
With the -fllvm backend:
Main_mainzuzdszdwfoldlMzuloop_entry: # @Main_mainzuzdszdwfoldlMzuloop_entry
# BB#0: # %c28E
subq $8, %rsp
movsd .LCPI3_0(%rip), %xmm0
jmp .LBB3_1
.align 16
.LBB3_3: # %n28K.i
# in Loop: Header=BB3_1 Depth=1
movapd %xmm0, %xmm5
cvtsi2sdq %rcx, %xmm8
addq $-2, %rsi
addq $2, %r14
subsd %xmm7, %xmm5
divsd %xmm8, %xmm5
addsd %xmm7, %xmm5
.LBB3_1: # %tailrecurse
# =>This Inner Loop Header: Depth=1
testq %rsi, %rsi
jle .LBB3_5
# BB#2: # %n28K
# in Loop: Header=BB3_1 Depth=1
movapd %xmm0, %xmm7
cvtsi2sdq %r14, %xmm8
leaq -1(%rsi), %rax
leaq 1(%r14), %rcx
subsd %xmm5, %xmm7
testq %rax, %rax
divsd %xmm8, %xmm7
addsd %xmm5, %xmm7
jg .LBB3_3
# BB#4: # %c28J.i
movq (%rbp), %rdx
movq %rcx, %rbx
movq %rcx, %r14
movq %rax, %rsi
movapd %xmm7, %xmm5
movq (%rdx), %r11
addq $8, %rsp
jmpq *%r11 # TAILCALL
.LBB3_5: # %c28J
movq (%rbp), %rax
movq %r14, %rbx
movq (%rax), %r11
addq $8, %rsp
jmpq *%r11 # TAILCALL
And running it:
$ time ./mean 3.141592653589793 ./mean 5.55s user 0.01s system 99% cpu 5.585 total
Some pretty wacky code, but a little faster.
Conclusions
The LLVM backend seems to be holding up to what we hoped: it does a better (some times much better) job on tight loops. We get better code than GHC has ever produced before. It seems pretty robust, so far everything I’ve tried has worked.
David’s benchmarks indicate that with the current — first attempt — at an LLVM backend most large programs aren’t noticeably faster, but I think the promise we see in these small examples justifies spending more time working on the LLVM backend to GHC. It has much more potential than the GCC backend.
Currently we’re not experimenting with the LLVM optimization layer at all — I think there’s likely to be a lot of win just tweaking those settings (and exposing them to the Haskell programmer via GHC flags).